Newton'sche Gesetze und deren Anwendungen
- Ein Bus mit einer Masse von 10 t fährt los und erreicht auf der Strecke 50 m die Geschwindigkeit 10 m/s. Ermitteln Sie die Reibungszahl, wenn die Zugkraft 14 kN beträgt.
![Lösung anzeigen]()
- Eine Straßenbahn (bestehend aus einem Triebwagen mit 17 t Masse und zwei Hängern mit je 14 t Masse) verlässt den Haltestellenbereich gleichmäßig beschleunigt. Ermitteln Sie:
a) Nach welcher Zeit erreicht sie eine Geschwindigkeit von 40 km/h, wenn die Antriebskraft 58,5 kN beträgt?
b) Welche Bremskraft ist notwendig, um die Bahn auf einer Strecke von 40 m zum Stehen zu bringen?
![Lösung anzeigen]()
- Mit welcher Beschleunigung gleitet ein Körper auf der geneigten Ebene (Neigungswinkel beträgt 30°), wenn die Reibungszahl 0,2 beträgt?
![Lösung anzeigen]()
- An einem Federkraftmesser ist eine feste Rolle befestigt. Zwei Körper mit Massen m1 = 50 g und m2 = 75 g sind mit einem Seil, das über der Rolle hängt, miteinander verbunden und werden festgehalten (auf die Masse der Rolle und des Seiles kann verzichtet werden). Nun werden die Körper losgelassen. Leiten Sie die Formel für die Ermittlung der Beschleunigung her und berechnen Sie:
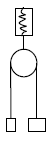
a) die Beschleunigung, mit der sich die Körper bewegen.
b) die Seilkraft.
c) die Anzeige vom Federkraftmesser.
b) den Abstand zwischen den Körpern nach 1 s.
![Lösung anzeigen]()
- Bei welcher Reibungszahl ist es "schwerer", den Körper entlang der geneigten Ebene hochzuziehen als senkrecht zu heben?
![Lösung anzeigen]()
- Ermitteln Sie die Beschleunigung, mit der sich die Körper m1 und m2 entlang der geneigten Ebene bewegen, und die Seilkraft (siehe Skizze). Auf die Masse der Rolle und des Seiles kann verzichtet werden ebenso wie auf die Reibung zwischen Körper und geneigte Ebene.
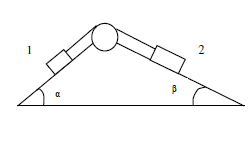
![Lösung anzeigen]()
- Wie ändert sich die wirkende Kraft im Seil, wenn der Körper 1 mit der Masse m1 zuerst auf Glas gleitet (μ = 0), dann auf Holz (μ ≠ 0) (siehe Skizze). Hinweis: ermitteln Sie ΔF.
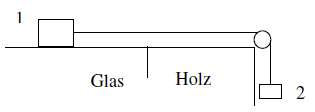
![Lösung anzeigen]()
- Zwei Körper (Massen m und M) sind mit einem Seil verbunden und liegen auf einer glatten Unterlage. Auf die Körper wirken Kräfte F1 und F2 (siehe Skizze). Leiten Sie Formeln her:
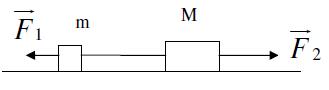
a) zur Ermittlung der Beschleunigung, mit der sich die Körper bewegen.
b) zur Ermittlung der Seilkraft.
c) Berechnen Sie a und Fs für m = 0,2 kg, M = 4 kg, F1 = 0,2 N, F2 = 0,5 N
d) Schätzen Sie ab, wie groß Fs aus der Teilaufgabe b) ist, wenn m << M
![Lösung anzeigen]()
- Der 1. Körper fällt frei, der 2. Körper gleitet ohne Reibung entlang der geneigten Ebene (Winkel α) Vergleichen Sie die Endgeschwindigkeiten und die Bewegungszeiten der 2 Körper.
![Lösung anzeigen]()
- Auf einer geneigten Ebene (α = 30°) befindet sich ein Körper mit der Masse 50 kg. Auf den Körper wirkt eine Kraft 300 N (siehe Skizze). Ermitteln Sie:

a) die Beschleunigung, mit der sich der Körper bewegt.
b) die Kraft, mit der der Körper auf die Ebene wirkt.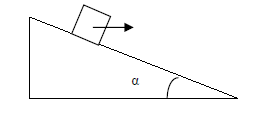
![Lösung anzeigen]()
- Ein Auto (mit abgestelltem Motor) fährt einen Hang (Winkel α) mit einer Anfangsgeschwindigkeit v0 hinauf. Ermitteln Sie den Weg, den das Auto bis zum Umkehrpunkt in der Zeit t zurücklegt, wenn die Reibungszahl μ ist.
![Lösung anzeigen]()
- Ein Wagen rollt eine 200 m lange Strecke, deren Gefälle 4% beträgt, abwärts und auf einer gleich großen Steigung anschließend wieder nach oben (Fahrwiderstandszahl μ = 0,03). Ermitteln Sie die Strecke x, die auf der Steigung zurückgelegt wird.

![Lösung anzeigen]()
- Ein Schlitten fährt vom Berg herunter und dann weiter waagerecht bis zum Stillstand. Die Reibungszahl ist auf der Gesamtstrecke μ. Ermitteln Sie s. (h und α sind gegeben)
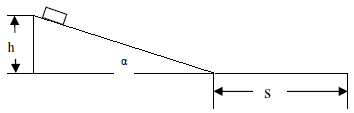
![Lösung anzeigen]()







