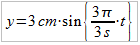Mechanische Wellen
- Dargestellt sind zwei eine Welle beschreibende Diagramme:
a) Entnehmen Sie den Darstellungen die Kenngrößen dieser Welle.
b) Bestimmen Sie die Frequenz und die Ausbreitungsgeschwindigkeit einer Wasserwelle.
c) Geben Sie die Wellengleichung an.
d) Wie lautet die Gleichung für einen Schwinger für x = 50 cm. 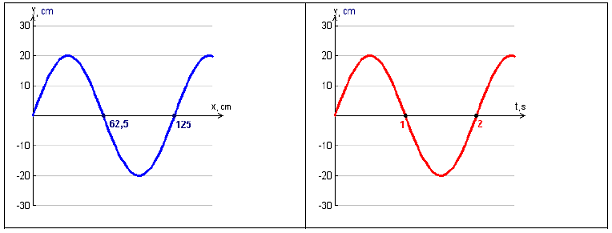
![Lösung anzeigen]()
- Für einen Schwinger einer Transversalwelle lautet die Schwingungsgleichung:
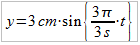 Der Schwingungszustand breitet sich mit einer Geschwindigkeit von 5,0 m/s aus.
Der Schwingungszustand breitet sich mit einer Geschwindigkeit von 5,0 m/s aus.
a) Wie groß sind Amplitude, Schwingungsdauer, Frequenz und Wellenlänge?
b) Geben Sie die Wellengleichung für diese Welle an.
![Lösung anzeigen]()
- Bei der Ausbreitung einer Schallwelle der Frequenz 2 kHz werden die Wellenlängen im Wasserstoff (ϑ = 20°C) , in der Luft (ϑ = 20°C) und im Mauerwerk gemessen. Sie betragen 0,64 m; 0,17 m und 1,80 m. Ermitteln Sie die Ausbreitungsgeschwindigkeiten der Schallwelle.
![Lösung anzeigen]()
- Von einem Schiff auf dem offenen Meer wird dicht unter der Wasseroberfläche ein Ultraschallimpuls ausgesandt. Das erste Echo wird nach 1,75 s empfangen. Ermitteln Sie die Meerestiefe an dieser Stelle, wenn die Schallgeschwindigkeit im Meerwasser 1400 m/s beträgt.
![Lösung anzeigen]()
- Der Mensch kann Frequenzen von etwa 20 Hz bis 16 kHz hören. Welchen Wellenlängen entspricht das in der Luft (v = 344 m/s)?
![Lösung anzeigen]()
- Wasserwellen bewegen sich in tiefem Wasser mit der Geschwindigkeit 0,18 m/s und haben die Wellenlänge 1,2 cm. Sie treffen unter dem Einfallswinkel 50° auf die Grenzlinie zu einem Gebiet mit flachem Wasser, wo sie sich mit 0,12 m/s bewegen.
a) Berechnen Sie den Brechungswinkel
b) Berechnen Sie die Frequenz und die Wellenlänge im flachen Wasser.
![Lösung anzeigen]()
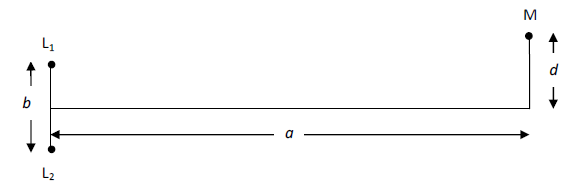
- Zwei Lautsprecher L1 und L2 im Abstand b = 40 cm erzeugen gleichphasig Schallwellen mit derselben Frequenz f. Im Abstand a = 1,5 m wird ein Mikrofon M senkrecht zur Symmetrieachse der beiden Lautsprecher bewegt. In der Entfernung d = 35 cm von der Symmetrieachse wird das Interferenzminimum 1. Ordnung festgestellt. Die Schallgeschwindigkeit beträgt 340 m/s. Berechnen Sie die Frequenz f der Schallwellen.
![Lösung anzeigen]()