Mechanische Schwingungen 2
- Ein Massepunkt schwingt nach dem Gesetz: y = 4 cm sin ( 2 π ( t + 0,25)). Ermitteln Sie: ymax, T, ω, φ0
![Lösung anzeigen]()
- Stellen Sie Gleichungen für folgende Schwingungen auf:
a) Eine Massepunkt schwingt mit der Frequenz 5 Hz, die Amplitude beträgt 0,5 m. Die Schwingung beginnt bei y0 = 0,3 m.
b) Eine Massepunkt schwingt mit der Periodendauer 2 s. Die Schwingung beginnt bei y0 = 0,5 ymax, nach t1 = 0,5 T ist der Massepunkt bei y1 = 0,5 m.
![Lösung anzeigen]()
- Die Membran eines Lautsprechers hat eine Masse von 6 g. Ihre Amplitude beträgt 0,1 mm. Ermitteln Sie die maximalen Geschwindigkeiten der Membran bei den Frequenzen 50 Hz und 5 kHz und die Schwingungsenergien.
![Lösung anzeigen]()
- Ein Fadenpendel und ein vertikaler Federschwinger schwingen auf der Erde mit einer Frequenz von 1 Hz. Ermitteln Sie ihre Frequenzen auf dem Mond.
![Lösung anzeigen]()
- Ermitteln Sie:
a) Die Länge eines Fadenpendels, das mit einer Periodendauer von 1 s schwingt.
b) Die Länge eines Sekundenpendels.
c) Die Periodendauer eines 1 m langen Fadenpendels.
![Lösung anzeigen]()
- Ermitteln Sie die Periodendauer einer vollen Schwingung des abgebildeten Fadenpendels der Länge l. Der Stift befindet sich bei l/2.
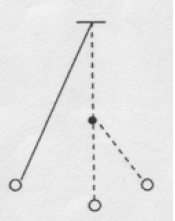
![Lösung anzeigen]()
- Ein U-Rohr mit Kreisförmigen Querschnitt hat den Radius r. In ihm befindet sich eine Flüssigkeitssäule mit der (in der Mitte gemessen) Gesamtlänge l. Die Flüssigkeit hat die Dichte ρ. Wenn man kurz in des eine Rohrende bläst, wird die Flüssigkeitssäule zu Schwingungen angeregt.
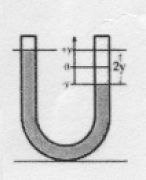
a) Zeigen Sie, dass die Flüssigkeitssäule harmonisch schwingt. Betrachten Sie dazu den abgebildeten Schwingungszustand.
b) Zeigen Sie, dass die Schwingungsdauer der Flüssigkeitssäule allein von ihrer Länge l abhängt.
![Lösung anzeigen]()
- Eine Kuckucksuhr gehe in Deutschland auf die Sekunde genau.
a) Wie wird dieselbe Uhr am Äquator gehen? Begründen Sie!
b) Gegebenenfalls ermitteln Sie die Abweichung von der genauen Zeit innerhalb von 24 Stunden.
![Lösung anzeigen]()

